磁性超结构的深度学习电子结构计算(AI文献阅读）

(2023-04) Deep-learning electronic-structure calculation of magnetic superstructures (磁性超结构的深度学习电子结构计算)

一、基础知识准备

1. 第一性原理计算（Density Functional Theory, DFT）

• 是什么：基于量子力学从头计算材料性质的方法，无需经验参数。

• 核心方程：Kohn-Sham方程[ -½∇² + V_eff(ρ) ] ψ_i = ε_i ψ_i 其中电子密度 ρ = Σ|ψ_i|²，V_eff 包含外场、库仑和交换关联势。

• 瓶颈：计算复杂度随原子数呈指数增长，对磁性超结构（如斯格明子）尤其严重。

2. 磁性体系基础

• 磁序类型：

• 关键效应：
• 拓扑霍尔效应：电子在实空间受拓扑磁结构散射产生的额外霍尔电导。
• 平带物理：能带色散消失，电子强关联导致超导/磁性等新物态。

3. 深度学习基础

• 等变神经网络（ENN）： 网络输出随输入对称变换（如旋转、平移）而协变。例如旋转分子后，预测性质自动匹配。

• 消息传递网络（MPNN）： 通过原子（节点）和键（边）的信息迭代更新，学习图结构数据（如分子、晶体）。

4. 专业工具

• 约束DFT：固定原子磁矩方向 {M} 计算哈密顿量 H_DFT（需额外计算资源）。

• 局域基组：用原子轨道线性组合表示波函数（如OpenMX中的伪原子轨道）。

二、论文精读：xDeepH方法

1. 问题瓶颈

• 传统DFT缺陷：计算磁性超结构（如斯格明子、摩尔磁体）时，因哈密顿量 H_DFT 依赖原子结构 {R} 和磁结构 {M}，计算成本过高。

• 现有深度学习局限：现有模型（如DeepH）忽略磁自由度，无法处理非共线磁序。

2. xDeepH解决方案

• 框架创新：
• 输入：原子位置 {R} + 磁矩方向 {M} → 输出：自旋轨道哈密顿量 H_DFT。
• 对称性嵌入：强制网络满足 E(3) × {I, T} 对称性（欧几里得变换+时间反演）。

• 网络架构：





• 磁矩层严格局域性：仅邻近原子磁矩影响 H_ij（与原子结构影响范围 R_N2 < R_N1 物理一致）。

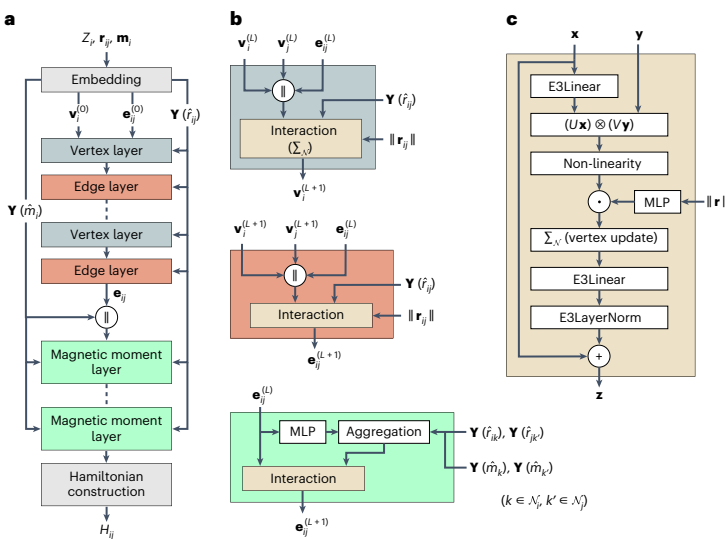
3. 关键物理原理

• 近视力原则（Nearsightedness）：H_DFT 矩阵元 H_ij 仅受局域环境（d_ij < R_C）影响，支持分块计算。

• 时间反演对称性：
• 操作 T: {M} → -{M}, H_DFT 虚部变号（公式2）。
• 网络通过奇偶索引 t=0/1 区分时间反演属性。

4. 性能验证

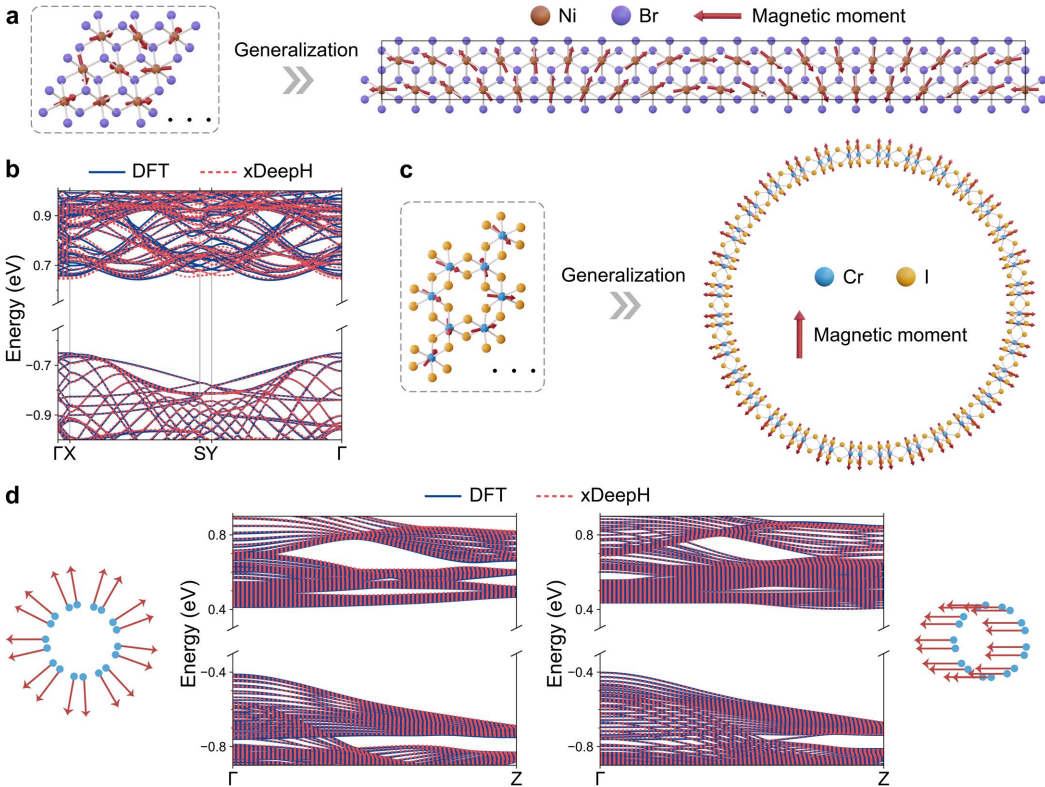
三、核心术语详解

1. 磁性斯格明子（Magnetic Skyrmion）

• 特性：非共线磁序，具有拓扑数 Q = ∫(∂_x m × ∂_y m)·m dxdy，抗外部扰动。

2. 等变神经网络（Equivariant Neural Network）

• 数学表述： 对旋转操作 R，满足 f(R·x) = D(R)·f(x)，D(R) 为群表示矩阵。

• xDeepH实现： 特征向量 x^l_m 按角动量 l 变换，通过Clebsch-Gordan系数张量积实现 l₁⊗l₂ → |l₁-l₂|⊕...⊕(l₁+l₂)。

3. 近视力原则（Nearsightedness Principle）

• 物理本质：多体系统中，局部性质（如电荷密度）仅受有限邻域影响。

• xDeepH应用：
• 原子结构影响范围 R_N1 ≈ 3×R_C（~6–10 Å）
• 磁结构影响范围 R_N2 ≈ R_C（~3–5 Å）

4. 约束DFT（Constrained DFT）

• 目的：固定磁矩方向 {M} 计算 H_DFT。

• 代价：需迭代求解约束场，计算量远大于非磁性体系（论文方法2.2节）。

5. 平带（Flat Band）

• 定义：能带色散 E(k) ≈ 常数，有效质量 m* → ∞。

• 意义： 在扭曲双层CrI₃中，磁斯格明子破坏平带（扩展图2c），暗示磁序与电子关联强耦合。

总结

1. 对称性嵌入：严格满足 E(3)×{I,T} 群变换

2. 物理引导架构：磁矩层局域性 + 双尺度近视力分离

3. 高效电子结构计算：为斯格明子、摩尔磁体等量子材料研究提供新工具。